Case Study Analysis of Database Construction for Smoke Control Simulation Experiments Using Scale Model

Hajun Im; Wonchang Kim; Keesin Jeong; Taegyu Lee

doi:10.7731/KIFSE.50cf89b1

Int J Fire Sci Eng > Volume 37(2); 2023 > Article

Im, Kim, Jeong, and Lee: Case Study Analysis of Database Construction for Smoke Control Simulation Experiments Using Scale Model

Research Paper

International Journal of Fire Science and Engineering 2023;37(2):12-19.

Published online: June 30, 2023

DOI: https://doi.org/10.7731/KIFSE.50cf89b1

Case Study Analysis of Database Construction for Smoke Control Simulation Experiments Using Scale Model

Hajun Im, Wonchang Kim, Keesin Jeong, Taegyu Lee^†

Department of Fire and Disaster Prevention, Semyung University, Choongbuk 27136, Republic of Korea

^†Corresponding Author, TEL: +82-43-649-1315, FAX: +82-43-649-1787, E-Mail: ltg777@semyung.ac.kr

Received May 10, 2023 Revised May 30, 2023 Accepted June 1, 2023

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

Most studies on fire properties, including smoke control, have been based on simulations. However, the results of simulation experiments have an average error rate of approximately 36.7%, and data with low reliability are obtained, compared to theoretical values and actual-scale measurements. In addition, experimental studies using scale models exhibit an average error rate of 6.9%, significantly lower than those of simulation experiments. In this study, a method for decreasing the error rate of simulation experiments was investigated by constructing a database using scale-model smoke control experiments.

Keywords: Smoke control; Error rate; Scale model; Simulation

1. Introduction

As the sizes of buildings increase owing to the rapid industrial development and advanced construction technology of modern society, emphasis on human safety is increasing [1]. Accordingly, studies on safety, including firefighting equipment, fire-resistant materials, and smoke control, are required.

Table 1 lists the statistics of fire accident deaths over the last five years reported by the National Fire Agency. Among the fire accident deaths, suffocation deaths caused by smoke and toxic gas inhalation represented more than 35.0%. The death rate reached 57.7% when smoke and toxic gases were accompanied by burns [2]. In this regard, identifying the characteristics of smoke has been emphasized, and studies on smoke flow and smoke control have been conducted. However, performing actual-scale smoke control experiments involves high costs and risk [3]. In most cases, computer simulations are used to identify the flow characteristics of smoke because of the nature of smoke control experiments that require the reproduction of buildings and setting of various conditions. Computer simulation is convenient, but the sufficient reliability of the data cannot be guaranteed. Kim et al. [4] compared Fire Dynamics Simulator (FDS) data with actual-scale experimental data obtained for a fire experiment. They reported that the error range increased, and low reliability was observed owing to insufficient data used in the simulation.

For scale-model experiments, data with higher reliability than those of simulation experiments can be obtained. Kim et al. [5] conducted a model experiment at a scale of 1:20 and assumed a fire inside a tunnel. They reported that the results of the experiment are applicable to actual tunnel designs because the experimental and numerical analysis results showed an error range lower than 10%. Scale-model experiments have been performed using limited models such as tunnels, and various types of materials are required to combine steel beams, acrylic materials, steel plates, cerakwool, and other materials [6].

Scale-model experiments are valuable methods for supplementing the error rate and improving the reliability of simulation results. Consistent data can be obtained when experiments on fire properties are conducted in actual space, but scale-model experiments enable a more detailed investigation than experiments in actual space through relatively convenient designs and preparation. Scale-model experiments minimize the error rate and validate the errors attributed to insufficient databases.

Performance-based design, which is an engineering-based approach to fire safety performance evaluation, has been implemented to overcome the limitations of existing uniform specification-based design methods. The fire safety performance of new buildings has been assessed using simulation software for performance-based design. Despite its convenience, simulations have disadvantages, such as inappropriate case selection, low reliability, and the absence of quantitative criteria for simulation input values [7,8]. Therefore, this study attempted to analyze the applicability of experiments on fire properties and smoke control by constructing a database for simulation experiments using scale-model experiments.

2. Research Trends and Error Rate Analysis Method

Table 2 lists the analysis of previous studies on fire. In these studies, experiments were conducted on various types of buildings. These studies used a 1:1 scale and reduced scales. For the 1:1 scale, experiments were conducted using actual space or simulations; for the reduced scales, models and simulations were used.

2.1 Analysis of previous studies on fire properties

For studies that used scale models, the minimum scale was 1:2.5, and the maximum scale was 1:50. The types of buildings analyzed for the scale-model experiments included tunnels [3,5,13,14,17-22,27], underground railway stations [6], parking lots [12], hydroelectric power plants [26], atrium [16], and cuboid rooms [23]. Most of the experiments were performed using tunnel-type models. This is possibly because it is easier to prepare tunnel-type models than other model types.

Previous simulation studies were based on scales ranging from 1:1 to 1:3. Most of these simulation studies were conducted in cuboid rooms [5], whereas some were conducted on vertical walls [8] and wood stacks [9]. For scale-model experiments, the temperature distribution and smoke flow were the main analyzed properties. In the case of the simulation studies, various data such as the heat release rate, heat flux, and CO, CO₂, and O₂ concentrations were analyzed.

Figure 1 shows an example of a smoke control experiment, Figure 2 shows an example of a simulation experiment with FDS.

2.2 Error rate analysis method

Table 3 lists a summary of the smoke control and heat experiments performed on actual scales, reduced models, and simulations. Most of the experiments were based on the tunnel type because the model construction was relatively convenient. For the tunnel-type model, experiments were conducted at a minimum ratio of 1:4 [27] and a maximum ratio of 1:40 [14]. In the case of the cuboid-type model, experiments were performed at a minimum ratio of 1:6 [15]. The most reduced experiment was performed for the atrium-type architecture with a ratio of 1:50 [16].

Eq. (1) was used to calculate the error rates in previous studies (Table 3). The measured values were obtained using the "Graph Data Extractor" software.

(1)

Theoretical value-measured valueTheoretical value×100=error rate (%)

The theoretical value is the actual-scale experimental value or the theoretically calculated value, whereas the measured value is the value obtained when a scale model or simulation was used.

3. Analysis Results

3.1 Error rate analysis results of previous studies

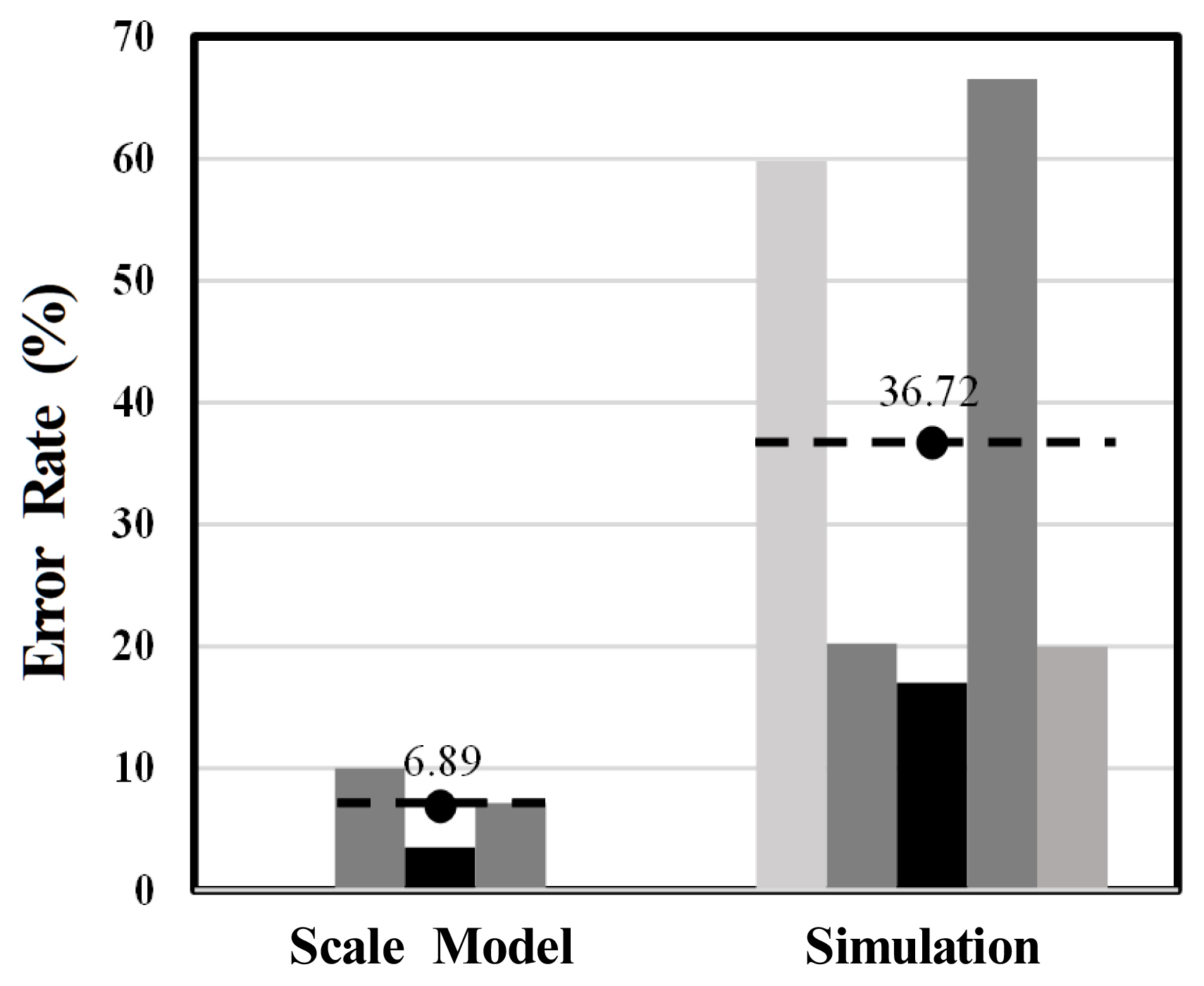
Figure 3 shows the error rates and average values of the experiments for which the error rates are calculated among the experiments listed in Table 3. The error rate was calculated by comparing the results of the scale-model experiments with the theoretical and actual-scale experimental results, and the same method was used for the simulation experiments. A comparison of the two experimental groups showed that the scale-model experiments yielded minimum and maximum error rates of 1.5% and 14.4%, respectively, whereas the simulation experiments yielded minimum and maximum error rates of 3.6% and 116.0%, respectively. The average error rates for the scale-model and simulation experiments were 6.9% and 36.7%, respectively. The scale-model experiments generally yielded lower error rates than the simulation experiments.

3.2 Results of analyzing formulas used in smoke control experiments

Table 4 lists the formulas used in previous scale-model experiments. Governing equations and the Froude scaling law were the most frequently used formulas in the studies. Among the governing equations, four types of continuity equations (mass conservation) and four types of momentum equations (momentum conservation) were used for the calculations. Scalar equations were expressed in two ways, and the equation of state was expressed in one way.

In the Froude scaling law, the heat release rate, velocity ratio, and time ratio were expressed as length-related equations. Although various expression methods are available, only one interpretation was expressed.

When the governing equations and Froude scaling law were considered, the widely used equations were as follows.

Scale-model experiments are performed by reducing the prototype building to a specified ratio. Therefore, compensation is determined according to the ratio using the Froude Scaling law to apply data to the prototype building:

(2)

VMVP=(LMLP)1/2=α

(3)

TMTP=(LM/VMLP/VP)1/2=α

(4)

QMQP=(LMLP)5/2=α5

where Q is the heat release rate, V is the flow velocity, L is the length, M is the model, P is the prototype, and α is the length ratio. The analysis of Eqs. (2) and (3) showed that the velocity ratio between the model and prototype was proportional to the square root of the length ratio. The time ratio was also proportional to the square root of the length because it is related to the velocity ratio. However, according to Eq. (4), the heat release rate was proportional to the length ratio to the power of 5/2.

The smoke analysis is governed by equations for density, mass, momentum, and scalar quantities. The governing equations used in previous experiments can be expressed as follows:

• Continuity equation

(5)

∂ ρ∂ t+∂∂ xi(ρui)=0

• Momentum equation

(6)

(∂∂ t(ρuj)+∂∂ xj(ρujui))=∂∂ xj(μeff(∂ ui∂ xj+∂ uj∂ xi))-∂ ρ∂ xi+ρgi

(7)

μeff=μ+μi

• Scalar equation

(8)

∂∂ t(ρ∅)+∂∂ xj(ρuj∅)=∂∂ xj(Γeff∂ ∅∂ xj)+S∅

• Equation of state

(9)

P=ρRT

where μ is the viscosity coefficient, μ_eff is the effective viscosity coefficient, and Γ eff is the effective diffusion coefficient. ø represents the temperature, smoke concentration, and velocity components. P is the pressure, ρ is the density, R is the specific gas constant, and T is the temperature. Subscripts i, j, and k indicate the x-, y-, and z-directions in the rectangular coordinate system, respectively.

4. Conclusion

In this study, a method for preparing a scale model and applying it to smoke control experiments was examined. The following conclusions were drawn.

1) Previous studies on smoke control analysis using simulations showed an average error rate of 36.7% and exhibited low reliability owing to insufficient databases. In contrast, scale-model experiments tended to exhibit higher reliability than simulation experiments, with an average error rate of 3.6%.

2) The equations used in previous studies on smoke control were governing equations and the Froude scaling law. If Eqs. (2)-(9) mentioned above are used in future scale-model and smoke control experimental research, it will be possible to obtain the error rate by calculating the theoretical value and comparing it with the measured value or simulation result. The equations are expected to help in constructing a more accurate database.

3) National laws and standards related to smoke control systems are insufficient compared to those of other countries. If data with lower error rates are applied to simulations using scale-model experiments based on the results of this study, it will be possible to assess the safety of buildings with higher reliability.

Acknowledgments

This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No.2022R1F1A1073333).

Notes

Conflicts of Interest

The authors declare no conflict of interest.

Author Contributions

Conceptualization, W.K. and T.L.; methodology, W.K.; software, W.K and K.J..; validation, W.K. and T.L.; formal analysis, H.I.; investigation, H.I.; resources, W.K.; data curation, H.I.; writing—original draft preparation, H.I.; writing—review and editing, W.K.; visualization, T.L.; supervision, W.K.; project administration, T.L.; funding acquisition, K.J. All authors have read and agreed to the published version of the manuscript.

Figure 1

Example of reduced-scale experimental setup[22].

Figure 2

Example of simulation experimental setup[4].

Figure 3

Error rates of scale models and simulation experiments.

Table 1

Number of Fire Accident Deaths (2018-2022)

Classification	Total	Smoke and Toxic Gases	Smoke, Toxic Gases, and Burns	Burns	Others
Total	2,996 (100%)	1,050 (35.0%)	679 (22.7%)	833 (27.8%)	434 (14.5%)
Building Structures	2,496	922	570	669	335
Ships and Aircraft	18	2	2	3	11
Gas Production Plants, etc.	8	0	0	2	6
Forests	82	22	17	29	14
Cars, Trains, Vehicles	302	86	74	91	51
Others	90	18	16	39	17

Table 2

Analysis of Smoke Control and Heat Experiments

Classification
Smoke Control and Heat Experiment	Experiment Method	Actual Scale (1:1) Experiment	Simulation[4,9-11]
		Actual Scale (1:1) Experiment	Actual Space[4,9,12]
		Reduced-Scale Model Experiment	Prototype Model[3,5,6,8,12-25]
		Reduced-Scale Model Experiment	Simulation[24-27]
	Form of Architecture	Tunnel Cuboid Room Atrium	Hydropower Plant Subway Building Vertical Wall

Table 3

Previous Fire Studies Using Reduced-Scale-Model and Simulation Experiments

Researchers	Model Type	Main Contents	Scale	Primary Measurement Items	Error rate
You et al. [3]	Tunnel	Reduced Model Test for Determination of Ventilation Velocity to Prevent Back Flow	1:20	Temperature Distribution CO Concentration	3.5% <
Kim et al. [5]		Growth and Movement of Smoke Layer in Tunnel, Temperature Distribution	1:20	Ceiling Jet Velocity Height of Smoke Layer	< 10%
Kim et al. [11]		Calculation of Critical Velocity based on Fire Intensity	1:29	Temperature Distribution Critical Velocity	< 15%
Bae et al. [27]	Cuboid Room	FDS for Pool Fires within Two Rooms	1:1	Heat Release Rate Temperature Distribution	< 20%
Kim et al. [4]		Reliability Analysis on FDS using Full-Scale Fire Experiment	1:1	Temperature Rise and Fall Time Heat Release Rate	36% <
Han et al. [14]		Fan Curve Model in FDS for Modeling of Mechanical Ventilation System	1:1	Temperature Distribution Heat Flux	< 25%
Park et al. [9]	Vertical wall	Simulation of Vertical Wall Fireusing FDS	1:1	Temperature Distribution Heat Flux	< 70%
Kim et al. [13]	Wood stack	Comparison between FDS Fire Model and Verification Experiments	1:1	CO and CO₂ Concentrations Heat Release Rate	< 39%

Table 4

Analysis of Governing Equations and Froude Scaling Law in Reduced-Scale-Model Experiments

Classification

Governing Equation

Froude Scaling Law

◎ Mass Conservation

∂ρ∂t+∂(ρuj)∂xj=Sm
∂∂xj(ρuj)=0
∂ρ∂t+∂(ρu)∂z+∂(ρν)∂y=0
LVτ∂ρ^∂t^+∂(ρ^y^)∂x^=0

◎ Momentum Conservation

(∂∂t(ρuj)+∂∂xj(ρujui))=∂∂xj(μeff(∂ui∂xj+∂uj∂xi))-∂ρ∂xi+ρgi
ρ(∂ν∂t+u∂ν∂z+ν∂ν∂y)=-∂p′∂y+g(ρ∞-ρ)+μΔν
ρ^(LVτ∂u^∂t^+u^∂u^∂x^)=-p*ρ0V2∂ρ^∂x^+43yρ0VL∂2u^∂x2^+gLV2(1-ρ^)

◎ Scalar Equation

∂∂t(ρ∅)+∂∂xj(ρuj∅)=∂∂xj(Γeff∂∅∂xj)+S∅
∂∂t(ρui)+∂∂xj(ρujui)=-∂P∂xi+∂∂xj(μeff∂uj∂xi)+ρgi

◎ Equation of State

P = ρRT

◎ Heat Release Rate Relationship

QMQP=(LMLP)52
QMQP=(LMLP)52=α5
QM=QF(lMlF)52
Q̈ ~ L^5/2

◎ Velocity Relationship

VMVF=(LMLF)12
VmVp=(LmLp)12=α
Frm=Vm2gLm=Vp2gLp=Frp
V_for_ced ~ L^1/2

◎ Time Relationship

TmTp=Lm/VmLp/Vp=α
tMtF=(LMLF)12

References

1. H. J. Kim, “Fire Safety of Buildings”, Architectural Institute of Korea Architecture, Vol. 57, No. 6, pp. 10-14 (2013).

2. National Fire Data System, https://nfds.go.kr .

3. Y. I. You and H. K. Lee, “The Reduced Model Test for the Determination of Ventilation Velocity to Prevent Backflow in Uni-directional Road Tunnel during a Fire Disaster”, Tunnel and Underground Space, Vol. 8, No. 2, pp. 107-117 (1998).

4. D. E. Kim, B. C. Kim, D. G. Seo, J. H. Lee and Y. J. Kwon, “A Reliability Analysis on FDS through Full Scaled Fire Experiment of a Sing Fire Area”, Proceedings of 2012 Spring Annual Conference, Korean Institute of Fire Science & Engineering, pp. 282-285 2012.

5. S. H. Kim, S. C. Kim, C. I. Kim and H. S. Ryou, “A Study of Smoke Movement in Tunnel Fires”, Fire Science and Engineering, Vol. 14, No. 2, pp. 21-32 (2000).

6. M. B. Kim and B. I. Choi, “An Experimental Study on Smoke Spread Using a Reduced-scale Subway Building Model”, Fire Science and Engineering, Vol. 22, No. 2, pp. 49-56 (2008).

7. H. M. Jeong, W. H. Hong, J. Y. Son and G. Y. Jeon, “A Study on Establishment of Performance-Based Design Direction through Analysis of Expert Survey”, Architectural Institute of Korea, Vol. 34, No. 2, pp. 23-31 (2018).

8. W. C. Park, “Shortcommings in Simulation of a Vertical Wall Fire by Using FDS”, Proceedings of 2008 Fall Annual Conference, Korean Institute of Fire Science & Engineering, pp. 68-75 (2008).

9. J. B. Kim, J. M. Lee and S. H. Min, “Study of the Reliability of the FDS Fire Model by Verification Experiments”, Journal of the Korean Society of Hazard Mitigation, Vol. 19, No. 1, pp. 197-203 (2019), https://doi.org/10.9798/KOSHAM.2019.19.1.197.

10. Y. B. Bae, S. H. Ryu, Y. I. Kim, S. K. Lee, O. H. Keum and J. S. Park, “Validation of FDS for the Pool Fires within Two Rooms”, Fire Science and Engineering, Vol. 24, No. 5, pp. 60-67 (2010).

11. H. S. Han, C. H. Hwang, Y. H. Jung and S. K. Lee, “A Study on the Application of Fan Curve Model in FDS for Modeling of Mechanical Ventilation System”, Transactions of the Korean Society of Mechanical Engineers B, Vol. 46, No. 1, pp. 41-50 No. 2022.

12. I. Horváth, J. V. Beeck and B. Merci, “Full-scale and Reduced-scale Tests on Smoke Movement in Case of Car Park Fire”, Fire Safety Journal, Vol. 57, pp. 35-43 (2013), https://doi.org/10.1016/j.firesaf.2012.10.009.

13. J. Y. Kim, K. B. Lim, T. B. Seo, D. H. Rie and J. O. Yoo, “A Study on the Calculation of Critical Velocity by F ire Intensity”, Fire Science and Engineering, Vol. 20, No. 4, pp. 91-97 (2006).

14. J. Y. Kim, Y. H. Jeon, T. B. Seo, J. O. Yoo and D. H. Rie, “A Study on Smoke Control Characteristic by the Effect of Jet Fan Installation Distance”, Fire Science and Engineering, Vol. 22, No. 1, pp. 16-23 (2008).

15. W. J. You and G. H. Ko, “Investigation of the Relationship Between Wall Thermal Conductivity and Inner Room Temperature in Compartment Fires”, Fire Science and Engineering, Vol. 32, No. 2, pp. 17-23 (2018), https://doi.org/10.7731/KIFSE.2018.32.2.017.

16. S. K. Ryu, C. I. Kim and H. S. Ryou, “The Experimental Study of Fire Properties in Reduced-scale Atrium Space”, Fire Science and Engineering, Vol. 13, No. 4, pp. 30-37 (1999).

17. S. R. Lee, “An Experimental Study on Smoke Movement by the External Wind in Road Tunnel Fires”, Tunnel and Underground Space, Vol. 24, No. 4, pp. 308-315 (2014), https://doi.org/10.7474/TUS.2014.24.4.308.

18. C. H. Hwang, B. H. Yoo, S. M. Kum, J. Y. Kim, H. J. Shin and C. E. Lee, “An Experimental Study of Smoke Movement in Tunnel Fire with Natural and Forced Ventilations”, Transactions of the Korean Society of Mechanical Engineers B, Vol. 29, No. 6, pp. 711-721 (2005), https://doi.org/10.3795/KSME-B.2005.29.6.711.

19. S. R. Lee, C. I. Kim and H. S. Ryou, “An Experimental Study of Smoke Movement in Tunnel Fires with Natural Ventilation”, Fire Science and Engineering, Vol. 15, No. 1, pp. 1-6 (2001).

20. S. R. Lee, C. I. Kim, H. S. Ryou, H. S. Kim and M. B. Jun, “An Experimental Study of Critical Velocity in Sloping Tunnel Fires”, Fire Science and Engineering, Vol. 18, No. 1, pp. 49-53 (2004).

21. K. B. Hong, J. Y. Na and H. S. Ryou, “Experimental Study on the Effect of the Area Ratio between Shaft and Tunnel and Heat Release Rate on the Plug-holing Phenomena in Shallow Underground Tunnels”, Journal of the Korea Academia-Industrial Cooperation Society, Vol. 20, No. 4, pp. 619-625 (2019), https://doi.org/10.5762/KAIS.2019.20.4.619.

22. H. G. Kim, D. S. Baek, J. H. Kim, S. W. Lee and J. O. Yoo, “Scaled model test for improvement and applicability of the transverse smoke control system on tunnels”, Journal of Korean Tunneling and Underground Space Association, Vol. 22, No. 5, pp. 563-574 No. 2020, https://doi.org/10.9711/KTAJ.2020.22.5.563.

23. S. C. Kim and G. H. Ko, “Characteristics of Heat Flux in a Compartment Fire - Reduced Scale Test”, F ire Science and Engineering, Vol. 25, No. 5, pp. 128-133 (2011).

24. G. H. Ko, “Numerical Study on the Validity of Scaling Law for Compartment Fires”, Fire Science and Engineering, Vol. 28, No. 4, pp. 29-34 (2014), https://doi.org/10.7731/KIFSE.2014.28.4.029.

25. H. S. Yun and C. H. Hwang, “Changes in Fire Characteristics according to the Distance Between the Fire Source and Sidewall in a Reduced-Scale Compartment”, Fire Science and Engineering, Vol. 33, No. 1, pp. 50-59 (2019), https://doi.org/10.7731/KIFSE.2019.33.1.050.

26. L. Huang, J. Ma, A. Li and Y. Wu, “Scale Modeling Experiments of Fire-induced Smoke and Extraction via Mechanical Ventilation in an Underground Hydropower Plant”, Sustainable Cities and Society, Vol. 44, pp. 536-549 (2019), https://doi.org/10.1016/j.scs.2018.09.021.

27. T. Wei, R. Zong, W. Zhao and J. Zhu, “Scale Model and Numerical Validation of Smoke Movement in Long-narrow Underground Fires”, Tunnelling and Underground Space Technology, Vol. 78, pp. 27-34 (2018), https://doi.org/10.1016/j.tust.2018.03.026.